La Efekto Dzhanibekov

Hodiaŭ io el la fizika kampo por la scivolemulo: La Efekto Dzhanibekov, ankaŭ konata kiel la tenisa rakedo-teoremo, klarigas nestabilecon de rotaciaj korpoj kun tri malsamaj momentoj de inercio. La momento de inercio indikas la reziston de korpo al ŝanĝoj en ĝia rotacia movado. Ĝi dependas de la aparta rotacia akso kaj de la geometrio. Kompreni la dinamikon de klasikaj hamiltonaj sistemoj ankoraŭ estas decida celo kun amaso da aplikoj, kiuj superas sian matematikan priskribon. En la kazo de integreblaj sistemoj kun malmultaj gradoj da libereco, efika aliro baziĝas sur geometria analizo por karakterizi la dinamikajn ecojn de la mekanika sistemo. Tiaj geometriaj fenomenoj estas tipe la origino de la fortikeco de iuj efikoj, kiuj povas esti observataj eksperimente. unu el ili estas la tiel nomata Efekto Dzhanibekov aŭ ankaŭ nomata la tenisa raketo-efiko.

Janibekov-efiko en la senpezeco de la ISS

Bonega kaj detala teoria derivaĵo de la fenomeno troveblas ĉi tie (https://arxiv.org/pdf/1606.08237.pdf). Ni traktas ĉi tie kun iu iomete pli kruda, sed kiu tamen klarigas la fenomenon. Bedaŭrinde, iu antaŭa scio pri la dinamiko de rigidaj korpoj necesas ĉi tie:

Konsideru matricon de inercio (diagonaligita) kun momentoj de inercio I1 kaj I2 kaj I3 tia ke I1 estas plej malgranda kaj I3 estas plej granda. Nun pripensu la movadon ĉirkaŭ la akso de la ĉefa momento de inercio I3. La angula rapido-vektoro estas:

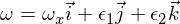
kie la epsilonoj estas malgrandaj perturboj en la aliaj du ĉefaj aksoj. Se vi nun enigas ĉi tion en la ekvaciojn de Euler, vi ricevas:

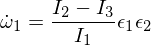
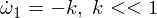
Nun ni diferencigas la duan Euler-ekvacion:

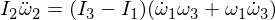
La anstataŭigo de omega 1 kaj omega 3 en nia esprimo, kaj ĉar multobligi la epsilonojn faras ilin sufiĉe malgrandaj por ignori,

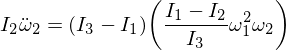
Ĉi tio donas al ni diferencialan ekvacion por Omega 2 de la formo:

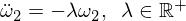
La baza solvo estas:

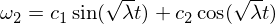
Tial ni scias, ke la rotacia malordo en la omega-1-akso estas stabila kaj faras periodajn movadojn, aŭ en la terminologio de rigida korpomovado, ke ĝi faras precesion. La omega 3-malordo sekvas similan argumenton kiel ĉi-supre, kaj mi lasos ĝin kiel ekzercon, por ke vi prilaboru ĝin. Por la meza akso ni havas:

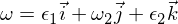
Enmetita en la Euler-ekvaciojn:

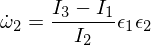
Diferencigi la trian Euler-ekvacion donas:

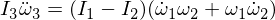
Ni anstataŭigu niajn derivitajn esprimojn:

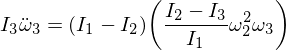
Nun rearanĝu kaj derivu la sekvan diferencialan ekvacion:

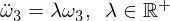
Rimarku, ke la koeficiento nun estas pozitiva, kio do kondukas al eksponentaj solvoj:

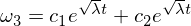
Ĉi tiu solvo montras, ke omega 3 estas malstabila laŭ la intera akso kun perturbo de omega 2!

Estis bedeutet das?

Nun ni povas kombini ĉion, kion ni derivis kaj lernis kompreni la teoremon. Por diri ĝin simple, se la rotacio laŭ la meza akso estas ĝenita, rezultas diferenciala ekvacio kun eksponentaj solvoj. Ĉi tio kondukas al malstabila movado, kontraste al la preciza movado observita en la aliaj du aksoj. Ĉi tiu rezulto estas sufiĉe surpriza. Ne ekzistas intuicia subteno por tia teoremo, ĉar ni ne povas imagi, kial la meza inercia momento rezultigus malstabilan rotacion. Ŝajnas, ke ĝi estas pure matematika.